Dessiner, c'est tricher ! En réalité, ne me faites pas dire que tous les dessinateurs sont des tricheurs, mais enfin... Qui d'entre nous n'a pas dessiné un personnage irréel, une maison inconstructible, un objet irréalisable ? Le dessin permet toutes les fantaisies, et Escher est passé maître en la matière.

Si vous avez visité l'espace diaporama de ce site, vous avez certainement remarqué les gravures "Cascade", "Belvédère", "Montée et descente", pour ne citer qu'elles. Au premier coup d'oeil, on ne fait qu'admirer la prodigieuse technique du dessinateur et du graveur. Ensuite, on doit se poser quelques questions...

Prenons comme exemple "Cascade". Que voit-on ?
La roue d'un moulin est actionnée par une chute d'eau. Rien que de très normal. Mais suivons le parcours de l'eau: elle est récupérée par un aqueduc, qui semble s'éloigner, et qui, après quelques virages, la ramène au sommet de la chute, d'où elle retombe !
Nous pouvons dire, et les scientifiques ne me démentiront pas, qu'Escher vient d'inventer le mouvement perpétuel (c'est d'ailleurs l'autre nom de la gravure), celui qui ne nécessite aucune énergie extérieure.

Mais comment a-t-il fait ?

Il a triché en dessinant, tout simplement, et nous nous proposons de découvrir et de démonter cette tricherie. En fait Escher est parti de la "tripoutre" du mathématicien anglais Penrose (ci-contre). Qu'est-ce qu'une tripoutre, me direz-vous ? Eh bien c'est une construction à trois poutres qui forment triangle.

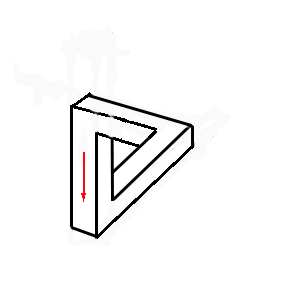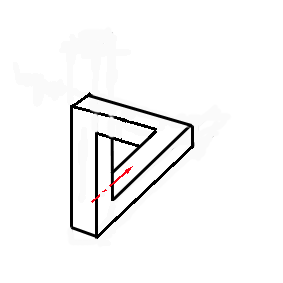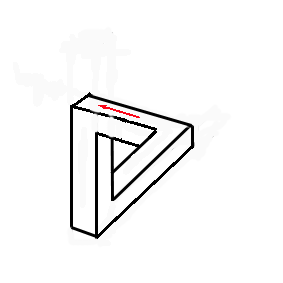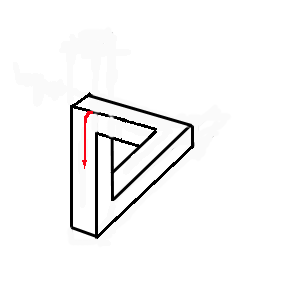
Pour la construire,on place une poutre par exemple verticalement (figure). Ensuite on dispose la deuxième poutre allant vers l'arrière puis la troisième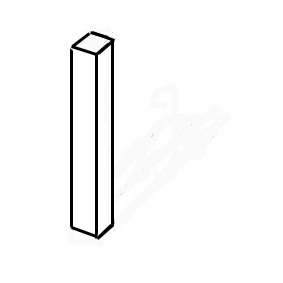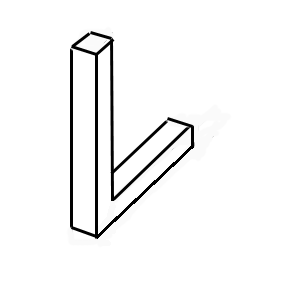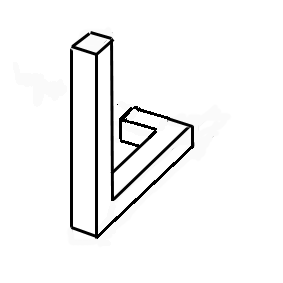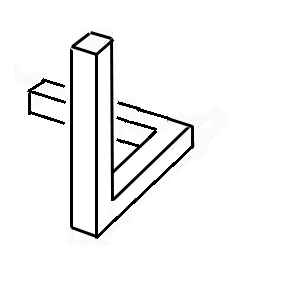 au bout de la seconde et allant vers la gauche. Difficile à comprendre ? Alors regardez la figure de gauche pour voir l'animation ! Selon notre logique, il est évident que la dernière poutre doit passer derrière la poutre verticale. Or Penrose propose d'abuser nos 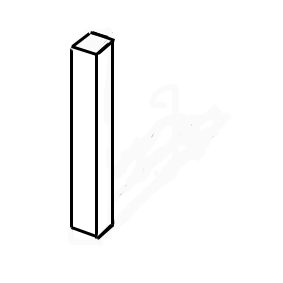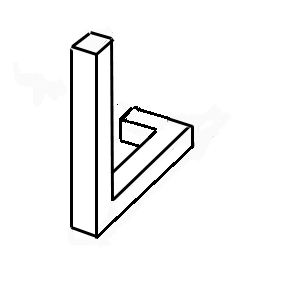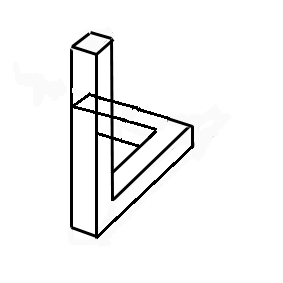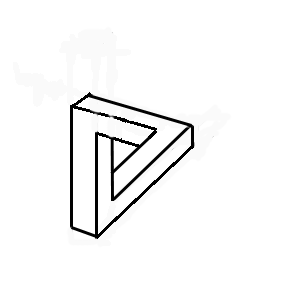sens en faisant rencontrer ces deux poutres.

Comment ? Regardez l'animation à droite. Les deux premières poutres sont disposées comme précédemment. La troisième rejoint la première en trichant sur le dessin. On obtient une figure qui semble normale à l'oeil, mais qu'il est impossible de construire : la tripoutre de Penrose. Si on place une flèche indiquant un sens de circulation (animation ci-après), on remarque la similitude avec la cascade d'Escher, les flèches représentant le mouvement de l'eau. La poutre verticale schématise la tour du dessin. La poutre du bas représente l'aqueduc inférieur, et la troisième l'aqueduc qui revient vers le premier étage de la tour. Compris ?

On comprend alors que le schéma de la cascade complète est la superposition de deux tripoutres identiques.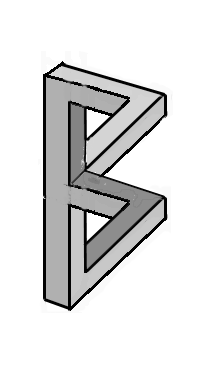 Remarquons qu'Escher possède un certain sens de l'humour puisque cette construction impossible ne semble pas déranger le moins du monde la dame qui étend son linge sur la droite de la gravure.

Et maintenant, amusez-vous avec ce petit puzzle à télécharger  (1,8 Mo)